CONTENIDOSYCOMPETENCIAS DE MATEMATICAS

Números entre cero y cualquier cantidad de dígitos.Practiquemos el ingles en matemáticas.....

Conjunto:Un conjunto es una agrupación de objetos, que poseen alguna característica en común. Pero no sólo nos referimos a cosas físicas, como lápices, libros, calculadoras, etc., sino también a elementos abstractos como números ó letras, entre otros
 A los objetos que conforman los conjuntos los llamamos elementos.

CLASES DE CONJUNTOS

Según el número de elementos que conforman un conjunto, éstos se clasifican en:

 Universal o referencia.

§  Vacío.

§   Unitario.

§   Finito.

§   Infinito.

 1. Conjunto universal o referencia

El conjunto universal o referencia, es el formado por un amplio número de elementos, como puede ser el conjunto de los números naturales o por letras del abecedario. Estos conjuntos sirven de base para crear más conjuntos.

Para representar que un conjunto es universal se utiliza la vocal Umayúscula.

Ejemplo:

El conjunto formado por las letras del abecedario.

U = { letras del abecedario }

Gráficamente:

Del conjunto U se puede formar el conjunto V de vocales y conjunto C de consonantes.

Conjunto vacío

El conjunto vacío es aquel que no tiene elemento alguno.

Ejemplos:

A = { }

El conjunto A no posee ningún elemento.

B = { números impares entre 5 y 7 }

No existe ningún numero impar entre los números 5 y 7.

Gráficamente:

Generalmente el conjunto vacío se representa mediante un paréntesis { } (corchete sin elemento), o por el símbolo .

 Conjunto unitario

 El conjunto unitario es aquel que posee solamente un elemento. 

Ejemplos:

1. El conjunto de números naturales mayores de 8 y menores de 10:

C = { 9 }

El único elemento es el número 9.

. Conjunto de satélites naturales de la Tierra

S = { Luna }

El conjunto está formado por un solo elemento, porque la Tierra solo posee un satélite natural, la Luna.

Conjunto finito 


Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras, es cuando los elementos del conjunto se pueden determinar o contar.

Ejemplos:

• Conjunto de números pares entre 10 y 40:

R = { 10,12,14,16,18,20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 }

• Conjunto de las páginas de un libro:

T = { páginas de un libro }.

• Conjunto de vocales.

V = { a, e, o, i, u }

Conjunto infinito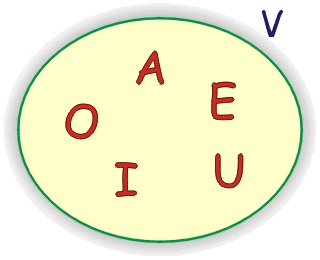 
El conjunto es infinito, cuando posee un inicio pero no tiene fin. Es decir, que la cantidad de elementos que conforman el conjunto no se puede determinar.

Ejemplos:

• El conjunto de los números naturales:

N = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,...}

El conjunto de los números naturales es infinito, puesto que no es posible contar la totalidad de elementos (números) que conforman el conjunto.

• El conjunto de los peces en el mar:

P = { los peces en el mar }

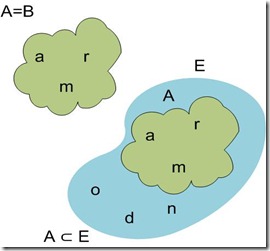
 Igualdad de conjuntos

Se dice que dos conjuntos son iguales si tienen exactamente los mismos elementos.  Una forma práctica de establecer si dos conjuntos son iguales es determinar si secontienen el uno al otro.

Observa los conjuntos todos los elementos de B pertenecen a A, es decir B = A. cuando la relación de inclusión es biunívoca, ósea, en ambos sentidos, se dice que A es igual a  y se representa por A=B.

Complemento de un conjunto: Complemento de un conjunto , es lo que le falta a un conjunto para ser igual al conjunto universal

Operaciones entre conjuntos

OPERACIONES CON CONJUNTOS

UNION

La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:

A È B = { x/x Î A ó x Î B }

Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }

A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }

INTERSECCION

Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }

Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:

A Ç B = { x/x Î A y x Î B }

Y se lee el conjunto de elementos x que están en A y están en B.

Ejemplo:

Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }

Q Ç P={ a, b, o, r, s, y }

DIFERENCIA

Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:

A - B={ x/x Î A ; X Ï B }

Ejemplo:

Sea A= { a, b, c, d } y

B= { a, b, c, g, h, i }

A - B= { d }

En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es

B – A = { g, h, i }

E indica los elementos que están en B y no en A.

DIAGRAMAS DE VENN

Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.

La manera de representar el conjunto Universal es un rectángulo, ó bien la hoja de papel con que se trabaje.

Un ejemplo de la representación del conjunto universal se muestra como:

Polinomios aritméticos

Un polinomio Aritmético es una expresión que combina las cuatro operaciones básicas. Aritmético hace referencia a que las operaciones involucran únicamente números.
Simplificar un polinomio aritmético tiene como finalidad la obtención del resultado de la expresión al efectuar todas las operaciones indicadas.
Valor de posición:Es el valor que tiene un dígito según la posición que ocupa en un número.

Observemos la tabla siguiente: Valor de posición de 23

2 Decena	=	20 Unidades
3 Unidad	=	3 Unidades

El valor de posición es el que tiene cada número de acuerdo a donde se encuentre ubicado dentro de la cantidad.
Por ejemplo, ¿cómo colocarías el número 19 dentro de la tabla de posición si cada casilla sólo acepta un número?
Es simple, tenemos que buscar con cuántas unidades se forma una decena. De las 19 unidades que tengo selecciono debo seleccionar 10, ya que esta cantidad representa 1 decena. Las unidades restantes las coloco en la casilla de las unidades.
Entonces la representación del 19 en la tabla de posiciones quedaría así:

CENTENAS	DECENAS	UNIDADES
	1	9

Otro ejemplo:
Tenemos el número 32
El dígito 3→  su valor posicional en la corresponde 30 unidades
El dígito 2→  su valor posicional corresponde a 2 unidades

Indica el valor del dígito destacado en cada caso:
17  = el número destacado es el 1, se encuentra en la posición de las decenas por lo tanto su valor es 10.
24  = el número destacado es el 4, se encuentra en la posición de las unidades por lo tanto su valor es 4.
8    = el número destacado es el 8, se encuentra en la posición de las unidades por lo tanto su valor es 8.
25  = el número destacado es el 2, se encuentra en la posición de las decenas por lo tanto su valor es 20.

Relaciones de orden

1. Son palabras que nos permiten entender comparaciones entre los números naturales y de esa forma poder ordenarlos según uno sea mayor, menor o igual que otro.
   Si un número es menor que otro tiene menos cantidad de cifras o números más pequeños. Si queremos ordenarlos de menor a mayor, debemos ubicar el menor a la izquierda y sucesivamente hacia la derecha, los mayores:
   >    : Mayor Que
   <    : Menor Que
   =    : Igual Que

 Los números se pueden ordenar de mayor a menor o viceversa.
 Para ordenar los números rápidamente podemos contar cuantos dígitos tienen.
Si tienen la misma cantidad de dígitos, debemos saber cuál está más cerca del cero y ese es el menor.
 Lo importante es saber que la punta del signo siempre tiene que mirar al número menor y la abertura mira al número mayor.
Algunos ejemplo:

Si te das cuenta no importa el orden de los números. Siempre la punta del signo está mirando al número 16, que en este caso es el menor.

Números romanos

 son aquellos que están representados por algunas letras del alfabeto latino, generalmente mayúsculas

Se emplea la numeración romana en los siguientes casos:

• En los siglos,
• Colón llegó a América a finales del siglo XV.

• En los nombres propios como son los de los papas, los reyes (y dinastías) y, excepcionalmente, personajes de linajes muy elevados desde el punto de vista social.

El papa Juan Pablo

• En congresos, ferias, olimpíadas, festivales, simposios, certámenes, etc.

• En libros, los volúmenes, las partes, cantos, capítulos, secciones y demás divisiones de una publicación.

Del mismo modo, se usan en los actos y escenas de una obra de teatro y para numerar las páginas de los prólogos y principios de un libro.

• En las siguientes divisiones militares (y según Martínez de Sousa no hay alternancia): armadas, cuerpos del ejército, agrupaciones o grupos, escuadrillas o grupos de infantería de marina, seciones de infantería de marina y escuadras de infantería de marina.

IV Cuerpo del Ejército, II Agrupación.

• Para las regiones militares.

III región Militar.

• En la denominación de las carreteras nacionales

• En la numeración de listas.

1: I

• 2: II
• 3: III
• 4: IV
• 5: V
• 6: VI
• 7: VII
• 8: VIII
• 9: IX
• 10: X

• 11: XI
• 12: XII
• 13: XIII
• 14: XIV
• 15: XV
• 16: XVI
• 17: XVII
• 18: XVIII
• 19: XIX
• 20: XX

• 21: XXI
• 22: XXII
• 23: XXIII
• 24: XX

• 25: XXV
• 26: XXVI
• 27: XXVII
• 28: XXVIII
• 29: XXIX
• 30: XXX

Logaritmo de la adicción

1. Que es la suma?  La suma o adición es una operación básica por su naturalidad, que se representa con el signo (+), el cual se combina con facilidad matemática de composición en la que consiste en combinar o añadir dos números o más para obtener una cantidad final o total. La suma también ilustra el proceso de juntar dos colecciones de objetos con el fin de obtener una sola colección. Por otro lado, la acción repetitiva de sumar uno es la forma más básica de contar.
2. 3. Para que se lo utiliza? ¨ La suma se utiliza para tomar la cuenta de los objetos que quieres calcular o para contar de una forma más fácil

 La suma tiene las siguientes propiedades:

Conmutativa: el orden de los sumandos no altera el resultado.

Por ejemplo: 2 + 3 = 3 +2

Asociativa: en una suma de 3 o más sumando se puede empezar sumado los 2 primeros y al resultado sumarle el tercero; o empezar sumando el segundo y el tercero y al resultado sumarle el primero.

3 + 5 +6 = (3 +5) +6 = 8 + 6 = 14

3 + 5 +6 = 3 + (5 +6) = 3 + 11 = 14

Elemento neutro: la suma tiene un elemento neutro que es el 0. Si se le suma 0 a cualquier número el resultado es el mismo número:

7 + 0 = 7

Cálculo de los elementos de la suma:

En una suma, cualquier sumando es igual al resultado (suma) menos los otros sumandos:

3 + 6 + 4 = 13

El primer sumando (3) es igual:

3 = 13 - 6 - 4

El segundo sumando (6) es igual:

6 = 13 - 3 - 4

 La resta o la sustracción es una operación matemática que se representa con el signo (-)

 Propiedades de la resta

Cálculo de los elementos de la resta:

El minuendo es igual a la suma del sustraendo y la diferencia:

10 - 7 = 3

El minuendo (10) es igual:

10 = 7 + 3

El sustraendo es igual al minuendo menos la diferencia:

12 – 8 = 4

El sustraendo (8) es igual:

8 = 12 - 4

 Propiedades y procesos de la adicciónn  

Prblemas  combinados con adicción y sustracción

Ayer Tomás compró una camiseta de$ 15000  y una mochila de $23ooo  pero le hicieron un descuento y, en total, solo pagó $35000  ¿Cuánto descuento le hicieron? 

                      

1. Tengo 125 pesos, si me he gastado 66 pesos. ¿Cuánto dinero me sobra?

A) 56

B) 69

C) 19

D) 59

2. Paloma me ha dado 18 dulces y Pedro la mitad que Paloma. ¿Cuántos dulces me han dado entre los dos?

A) 9

B) 5

C) 27

D) 13

3. ¿Cuántas entradas de 5 pesos puedo comprar con 10 billetes de 5 pesos?

4. El lunes me dieron 200 pesos, el martes 1000  y el miércoles 3000. Si el jueves gasté  1.200  pesos, ¿cuántos me quedan?

A)   1500

B) 2000

C) 3.000

D) 1.100

5. En una fiesta había 57 chicos y 30 chicas, ¿cuántos chicos había más que chicas?

6. ¿Cuánto costarán 5 bolígrafos a 3 pesos cada uno?

A) 18

B) 15

C) 14

D) 25

7. Marta quiere hacer 3 ramos de flores. Si en cada ramo pone una docena, ¿cuántas flores necesitará?

A) 26

B) 46

C) 36

D) 35

8. En un tren había 328 personas, si descendieron 178, ¿cuántos pasajeros quedaron en el tren?

9. En una granja había 2500 huevos, se estropean 1254 huevos, ¿Cuántos huevos quedan?

A) 1247

B) 1246

C) 1165

D) 1245

10. Rita saltó la cuerda 44 veces seguidas sin equivocarse y Mónica lo hizo 35 veces. ¿Cuántos saltos menos que Rita dió Mónica?

A) 11

B) 9

C) 8

D) 10